Claro que isso implica em (muito) mais sequências de movimentos a serem memorizadas, mas vale a pena. Abaixo estão as 4 partes básicas do método:
Cruz
O procedimento é o mesmo do método básico. Posicionar 4 peças de meio em volta do centro respectivo, com as cores adjacentes também corretas em relação aos seus centros.
 2 Primeiras Camadas
2 Primeiras CamadasNessa parte, diferente do método básico, você preenche as 2 camadas mais diretamente. Ao invés de posicionar os cantos da primeira camada e depois os meios da segunda, os pares de cantos e meios são posicionados.
Pode parecer meio complicado a princípio, mas você pode "descobrir" os algoritmos pra fazer isso. Se você não conseguir ou não quiser achar seus próprios algoritmos, eu coloquei os que eu uso nessa página.
Esse são os algoritmos pra se resolver as 2 primeiras camadas. Os códigos ao lado (A1, R2, S2) são usados no "Team blindfold", em que uma pessoa fica vendada e com o cubo, enquanto a outra dá as intruções. Pra não ter que falar todos os movimentos (R U R' U'...), criaram esses códigos.
Clique na imagem ou no texto para abrir o applet (cubo animado), em caso de dúvida.
Código Desenho Algoritmo
A1 U (L' U L) U2' (L' U L)
A2 U' (R U' R') U2 (R U' R')
A3 (R U R' U') (R U R' U') (R U R')
B1 (R U2' R U R' U) (R U2' R2)
B2 (R2 U2') (R' U' R U') (R' U2 R')
C1 U (L' U' L) d' (L U L')
C2 U' (R U R') d (R' U' R)
C3 (R U' R') y (L' U2 L)
D1 (R U' R')(F' L' U2 L F)
D2 (F' L' U2 L F)(R U R')
D3 (R U' R') d (R' U2' R U2') (R' U R)
"The Move Twice" (R U R' U') (R U R')
Good E (R U' R' U) (R U' R')
E3 (U' L' U L) d (R U' R')
"Lefty Move Twice" (L' U' L U) (L' U' L)
Good F (L' U L U') (L' U L)
F3 (U R U' R') d' (L' U L)
I1 (U' L' U L)
I2 (U R U' R')
J1 (U L' U2 L) d' (L U L')
J2 (U' R U2' R') d (R' U' R)
K1 U' (R U' R' U) (R U R')
K2 U (L' U L U') (L' U' L)
L1 (R U' R' U) d (R' U' R)
L2 (L' U L U') d' (L U L')
M1 (R U2' R') U' (R U R')
M2 (L' U2 L) U (L' U' L)
N1 (U2' L2 U2) (L U L' U L2)
N2 (U2 R2 U2) (R' U' R U' R2)
Nathan's A (R U R')
Nathans's E (L' U' L)
Q1 U (L' U' L U2') (L' U L)
Q2 U' (R U R' U2) (R U' R')
R1 U' (R U R' U) (R U R')
R2 U (L' U' L U') (L' U' L)
S1 d (R' U2 R U2') (R' U R)
S2 d' (L U2 L' U2) (L U' L')
Split 1,1 (R U R' U) (R U' R')
Split 1,2 (R U2' R' U) (R U' R')
Split 2,1 (L' U' L U') (L' U L)
Split 2,2 (L' U2 L U') (L' U L)
Orientação da última camada
Nessa etapa, o objetivo é fazer com que a face de cima fique toda de uma mesma cor, não importando ainda o posicionamento das peças. São 57 casos diferentes, que estão nessa página.
Permutação da última camada
Nessa etapa vamos terminar o cubo, posicionando as peças da última camada. São 21 casos diferentes. Os algoritmos que eu uso estão nessa página.
Boa sorte!

 possibilidades.
possibilidades.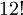 possibilidades.
possibilidades. possibilidades. O mesmo deve ocorrer com as arestas, pois aparecem mais
possibilidades. O mesmo deve ocorrer com as arestas, pois aparecem mais  possibilidades.
possibilidades. = 43.252.003.274.489.856.000
= 43.252.003.274.489.856.000








Casino & Resort - Mapyro
ResponderExcluirCasino & Resort. 3121 Boulder Highway, NV 89449. Directions · 전주 출장마사지 (775) 942-3100. Call Now · More Info. Hours, Accepts 원주 출장마사지 Credit Cards, 대전광역 출장마사지 Wi-Fi, 순천 출장샵 PokéStop, 춘천 출장안마 PokéStop, Rating: 2.3 · 3,431 votes