Algumas maneiras de melhorar sua velocidade na hora de montar o cubo:
Nas duas primeiras camadas
Na última camada
--------------------------------------------------------------------------------
Duas Primeiras Camadas (First Two Layers)
Você pode agilizar bastante o processo de construção das duas primeiras camadas usando um "truque" simples, que é o do "working corner", ou seja, "canto trabalhador".
Ele consiste em deixar um dos cantos da primeira camada "vazio". Dessa forma, você pode usar esse espaço para posicionar as peças da segunda camada mais facilmente.
Com esse espaço para trabalhar, as peças da segunda camada podem ser posicionadas com bem menos movimentos, o que gera ganho de velocidade
A idéia é simples: você gira a camada de baixo pra posicionar o canto vazio embaixo da posição da camada do meio que vai preencher. Então posiciona a peça da camada do meio. Depois gira novamente a camada de baixo até outra posição e posiciona aquela peça. Use essa tática até ter 3 meios da segunda camada posicionados. Veja o exemplo para entender como funciona o processo.
Resolução:
O canto vazio já está embaixo da posição do vermelho/azul. Então é só fazer F' U F para resolvê-lo. Não se preocupe com o canto branco/azul/vermelho agora.
Agora deslocamos o espaço na 1ª camada para DRB, fazendo u, e resolvemos o meio verde/vermelho com F' U2 F
Deslocamos de novo o espaço, agora com u2, e resolvemos o meio azul/laranja fazendo R U R'
Agora temos 3 cantos e 3 meios resolvidos. Agora use o espaço na camada do meio e resolva o canto branco/azul/vermelho (u' F' U' F U F' U' F).
Alinhe a primeira camada com os centros e resolva o meio que está faltando (D2 U2 R U' R' U' F' U F)
Agora você tem as 2 camadas prontas, e usou 28 movimentos. Se fizesse pelo método básico, usaria 33. Não é uma diferença muito grande no número, porque o último canto caiu no lugar mas virado errado. Mas essa forma é mais fácil de fazer
A solução completa ficaria:
(F' U F)
(u F' U2 F)
(u2 R U R')
(u' F' U' F U F' U' F)
(D2 U2 R U' R' U' F' U F)
Agora um exemplo completo. Vou usar o scramble B U2 R2 D' B' F D2 L' R D' U2 L' D' B L' R2 D R' B2 F2 L' D' F2 R2 D2. Seu cubo deve ficar assim:
Resolução:
Médio Nº Básico Nº
cruz: L' R' D B L F D 7 cruz: L'R' D B L F D 7
1º canto : y L' U' L 3 1º canto : y L' U' L 3
2º canto: U R U R' 4 2º canto: U R U R' 4
3º canto: y' U L' U' L 3 3º canto: y' U L' U' L 3
1º meio: D2 R U' R' 4 4º canto: y' U2 L' U L 4
2º meio: u R U2 R' 4 1º meio: y2 L' U L U F U' F' 7
3º meio: u F' U F 4 2º meio: y' L' U L U F U' F' 7
4º canto: D U R' U' R 4 3º meio: y' U L' U L U F U' F' 8
4º meio: D' y2 L' U L U F U' F' 8 4º meio: y' U2 L' U L U F U' F' 8
Total 40 Total 50
--------------------------------------------------------------------------------
Última camada
Essa parte pode ser agilizada aprendendo-se os algoritmos de permutação, que podem ser encontrados aqui. Dessa forma, você pode fazer a permutação da última camada sempre em 1 algoritmo, ao invés de ter que usar 2, 3 ou até 4.
Logicamente que isso requer mais memorização, então se você não quer "queimar neurônios" demais, pode aprender apenas alguns, que achar mais fáceis.
O Cubo Mágico
Descrição
O invento, descendente dum protótipo 2x2x2, criado por Larry Nichols (Lavourensis Plenus) em Março de 1970, é um quebra-cabeça que consiste num cubo. Cada uma das suas seis faces está dividida em nove partes, 3x3, num total de 26 peças que se articulam entre si devido ao mecanismo da peça interior central, oculta dentro do cubo.
[editar]História
O primeiro protótipo do cubo foi fabricado em 1974 quando Ernő Rubik era professor do Departamento de Desenho de Interiores da Academia de Artes e Trabalhos Manuais Aplicados de Budapeste (Hungria). Quando Rubik criou este quebra-cabeça, a sua intenção era criar uma peça que fosse perfeita, no que se refere à geometria, para ajudar a ilustrar o conceito da terceira dimensão aos seus alunos de arquitetura. A primeira peça que realizou foi em madeira e pintou os seus seis lados com seis cores distintas, para que, quando alguém girasse as faces do cubo, tivesse uma melhor visualização dos movimentos realizados.
[editar]Número de combinações possíveis no cubo de Rubik
- Por uma parte podemos combinar entre si, de qualquer forma, todos os vértices, o que dá lugar a
possibilidades. - Também temos as combinações dos cubos das arestas que são 12, existindo assim
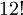possibilidades.
Entretando, apenas metade dessas possibilidades são verdadeiras, uma vez que não é possível trocar duas arestas de lugar sem trocar também a posição de dois vértices, ou vice-versa.
Além disso, podemos girar todos os vértices, salvo um, sem mudar nada mais no cubo. A orientação do último vértice será determinada pela que orientação dos outros sete, e isto cria 
possibilidades. O mesmo deve ocorrer com as arestas, pois aparecem mais 
possibilidades.
No total, o número de combinações possíveis no Cubo de Rubik é:
= 43.252.003.274.489.856.000[3]
Se alguém pudesse realizar todas as combinações possíveis a uma velocidade de 1 movimento por segundo, demoraria 1400 trilhões de anos, supondo que nunca repetisse a mesma combinação.[4]
[editar]Teorias sobre a Resolução
O cubo de Rubik é um teste básico para problemas de busca e enumeração." diz Gene Cooperman . "Busca e enumeração é uma enorme área de pesquisas, abrangendo muitos pesquisadores trabalhando em diferentes disciplinas - da inteligência artificial às operações. O cubo de Rubik permite que os pesquisadores de diferentes disciplinas comparem seus métodos em um problema único e bem conhecido.
Os movimentos executados para resolver o cubo, na realidade são comutadores, definidos pela fórmula:
[a,b] = a * b * a ^ (-1) * b ^ (-1)
[editar]Solução ótima
Utilizando a teoria dos grupos, Gene Cooperman e Daniel Kunkle testaram não apenas movimentos individuais, mas também grupos de movimentos, de forma a otimizar a solução. Foram 100 milhões de movimentos por segundo, até chegar ao resultado final.
E parece haver espaço para melhorias nos cálculos. Em 1997, o professor de ciência da computação Richard Korf afirmou que a solução ótima para o cubo de Rubik é de 18 movimentos. Até então, o melhor método, chamado de método Fridrich, elaborado por Jessica Fridrich, possibilitava a resolução do cubo em menos de 1 minuto.
[editar]Algoritmo de Deus
Um algoritmo que conseguisse resolver qualquer cubo de Rubik no menor número de movimentos possíveis é designado por "algoritmo de Deus", assim denominado porque, supostamente, seria necessário ter sabedoria de um ser superior para realizar tal proeza. Em 2005, o menor número de movimentos para resolver o cubo era de 28. Em 2007, passou a 26. [5] Em 2010, foi provado que o número exato é 20.[2]Para chegar a esse cálculo, alguns matemáticos, um engenheiro do Google e um programador dividiram o problema em 2.217.093.120 partes. A partir daí, os pesquisadores usaram a infraestrutura da companhia americana para processar os dados, chegando à conclusão.[6]
[editar]Permutações, grupos e as Configurações do Cubo
Uma permutação é um rearranjo de um conjunto de objetos. Matrizes são convenientes para descrever permutações. Mas há um modo mais simples: a notação de ciclos. Um ciclo pode ser pensado como uma série de transições de estado que acaba por retornar ao estado inicial.
S1 → S2 →…→ Sn → S1 Os movimentos R; L; F; B; U; D permutam o conjunto das facetas. Um fato importante surge quando usamos a notação de ciclos: toda permutação se decompõe como "produto" de ciclos disjuntos.
[editar]Aplicação Prática
Uma das possíveis aplicações práticas desse algoritmo é, por exemplo, na Criptografia de Dados através da Permutação.
[editar]Recorde
O recorde mundial de menor tempo para solucionar o enigma do cubo mágico é de 5.66s conseguido pelo australiano Feliks Zemdegs em janeiro de 2011.[7]
[editar]Variantes
Algumas variantes do cubo de Rubik:
Foram também criados versões 6×6×6 e 7×7×7, foram inventados por Panagiotis Verdes e são hoje vendidos pela V-Cubes.
[editar]Outras variantes
Outras das variantes consistem em interligar o poliedro utilizado. Na maioria foram inventadas por Uwe Mèffert:
Nenhum comentário:
Postar um comentário