Se você ainda não sabe resolver o cubo, fica muito difícil tentar fazê-lo sem olhar. Recomendo que você primeiro aprenda pelo menos o método básico antes de tentar esse aqui.
Introdução
Como a cada giro você mexe 20 adesivos, fica muito difícil acompanhar o que muda a cada mexida. Então, esse método pra resolver sem olhar é diferente dos outros. O cubo é resolvido em pequenas partes, só algumas peças de cada vez. Por isso é importante escolher uma orientação fixa do cubo, que você vai usar sempre. Eu uso o amarelo em cima e o azul na frente. A partir daí, as peças são resolvidas. Esse método que eu uso é dividido em 4 partes: orientação dos cantos, orientação dos meios, permutação dos cantos e permutação dos meios.
Algumas pessoas usam números pra facilitar a memorização. Eu uso esses números:
Cantos
1 UFL
2 UFR
3 UBR
4 UBL
5 DFL
6 DFR
7 DBR
8 DBL

Meios
1 UF
2 UL
3 UB
4 UR
5 FL
6 BL
7 BR
8 FR
9 DF
10 DL
11 DB
12 DR

Boa sorte!
Orientação dos cantos
Nessa primeira etapa, os cantos são girados pra ficarem com a cor de cima ou de baixo no seu lado de cima ou de baixo. No meu caso, a cor de cima é amarelo e a de baixo é branco. Então, eu tenho que girar os cantos pra deixá-los com seu adesivo amarelo/branco em cima ou embaixo. Veja o exemplo:
Usando esse scramble: L2 B D2 U' F U' B D2 B' D' B2 F2 D U B' L2 B2 U2 B' R' B D2 F2 R L2, os cantos ficam assim
Nesse caso, o canto 1 tem que girar no sentido anti-horário, o 2 também, o 3 está certo (amarelo em cima), o 4 gira no sentido horário, o 5 no anti-horário, o 6 no horário, 7 está certo (amarelo embaixo) e o 8 gira no sentido horário.
Certo...mas...como eu oriento? Os cantos são orientados em pares (em que cada canto gira em um sentido), trios (os 3 giram no mesmo sentido) ou grupos de 4. Pra isso eu uso algumas sequências de movimentos:
Ambos giram os cantos 2 e 3, só que em sentidos diferentes.
Esses merecem uma explicação. No da esquerda, a primeira parte, (R' U' R U)*2, gira o canto 1 no sentido horário. A segunda, (U' R' U R)*2, gira o canto 1 no sentido anti-horário. Os giros da camada L são usados pra colocar outro canto na posição 1 (no caso foi o canto 5), e girá-lo junto com o 1. No da direita, a mesma sequência (R' U' R U)*2 é usada, mas 3 vezes, para girar 3 cantos no sentido horário. O primeiro L traz o canto 4 para a posição 1, o segundo L traz o canto 8 para a posição 1 e o L2 no final volta todos para seus lugares.
Os próximos são mais avançados. Você consegue resolver bem qualquer caso usando esses, mas se quiser ser o mais eficiente possível, os algoritmos a seguir ajudam bastante. Clique no + para abrir a janela.
Avançados [+]
A primeira parte orienta os 4 cantos. A segunda volta os meios para seus lugares.
Duas formas de resolver o mesmo caso.
Ok...mas você deve estar pensando: "Tá, mas nem sempre os cantos estão nos lugares certos pra eu aplicar os algoritmos...". Certo. Então, são necessários o que chamamos de "setup moves". Ou seja, movimentos que deixam as peças que interessam em uma posição em que é possível orientá-las. Voltemos ao exemplo:
L2 B D2 U' F U' B D2 B' D' B2 F2 D U B' L2 B2 U2 B' R' B D2 F2 R L2
Uma forma de orientar os cantos seria:
1º - os cantos 1 e 4. Fazendo U2, eles ficam no lado direito. Aí é só aplicar a sequência e depois U2, pra voltá-los ao seu lugar correto.
2º - os cantos 5 e 6. Os setup moves necessários seriam F2 U', pra colocá-los no lado direito e em cima. Aplicamos a seqüência e desfazemos os setup moves, com U F2.
3º - os cantos 2 e 8. O setup seria B2, depois a seqüência, depois B2 novamente.
Esse foi só um exemplo. Os setup moves que você pode usar nessa fase são livres. Você pode orientar os cantos 2 e 7, por exemplo, fazendo B e uma das seqüências e depois B'. Ou F', ou ainda R' U. Só lembre-se de desfazer os setup moves depois dos algoritmos.
Orientação dos meios
Essa próxima etapa orienta os meios. É um pouco chato no começo, até entender quais estão certos e quais estão errados, mas quando se aprende, essa parte é mais fácil que a orientação dos cantos.
O conceito básico de um meio orientado corretamente é assim: "se ele pode ser colocado em sua posição com U(U' ou U2), D(mesmo do U), F(idem ao D), B(idem), L2 ou R2 (esses dois últimos limitados a meia volta)". Meio complicado, não? Mas na verdade é simples. Você pode mexer U, D, F e B o quanto quiser, mas L e R somente meia volta. Se conseguir colocar o meio X no seu lugar (e orientação, claro) correto dentro desses movimentos, ele está orientado. Se não, você precisa orientá-lo.
Agora um "truque" pra facilitar a identificação. Você vai procurar sempre pela cor mais clara de cada peça do meio. Se ele tiver amarelo ou branco, olhe essa cor. Se não tiver, olhe o vermelho ou laranja. O applet abaixo mostra onde as cores mais claras estão quando os meios estão orientados corretamente (as partes mais escuras).
(use o mouse para girar o cubo)
Explicando com palavras:
Na camadas de cima e de baixo, a cor mais clara tem que estar virada para cima ou para baixo. Na camada do meio, a cor mais clara tem que estar virada para a esquerda ou para a direita.
Se a cor mais clara do meio estiver em outro lugar, significa que ele está "errado".
Agora que você já sabe identificar quando um meio está certo ou errado, só falta aprender como deixar os que estão errados na orientação certa. Pra isso eu uso basicamente 2 seqüências. Uma vira 2 peças e a outra vira 4.
Assim como nos cantos, os meios nem sempre (quase nunca, na verdade) estão nessas posições. Então é preciso usar setup moves, pra deixá-los todos na mesma camada. Essa camada não precisa ser a de cima. Você pode usar as seqüências de qualquer ângulo, na frente, na esquerda, embaixo. Vamos a um exemplo. Usando o mesmo scramble que usamos na orientação dos cantos, os meios ficam assim:
L2 B D2 U' F U' B D2 B' D' B2 F2 D U B' L2 B2 U2 B' R' B D2 F2 R L2
Os meios errados, nesse caso, são 2, 3, 4, 6, 8 e 12. Eu resolveria da seguinte forma:
2 3 4 e 8: F'(setup move), (M' U)*4 (M U)*4, F(desfazendo o setup move)
6 e 12: x2 (girando o cubo no sentido de R 2 vezes), U' F (setup moves), (M' U M' U M' U2) (M U M U M U2), F' U (desfazendo os setup moves), x2 (voltando o cubo à orientação original
Novamente os setups nessa fase são livres. Você pode fazer qualquer movimento para posicionar os meios em uma posição favorável, desde que se lembre de desfazer esses movimentos após o algoritmo.
Permutação dos cantos
O próximo passo é colocar os cantos em seus lugares corretos, mas sem mudar sua orientação. Não adianta colocar o canto branco/azul/vermelho entre esses 3 centros mas girado errado. Essa etapa é bem simples. Os algoritmos usados são aqueles que permutam apenas os cantos. Eu uso esses:
Permutação dos meios
Essa parte é parecida com a dos cantos. Os ciclos são feitos da mesma maneira, e resolvidos com o mesmo princípio, ou seja, o ciclo (a b c d e f g) é feito como (a b c), (a d e), (a f g). Os algoritmos usados mudam apenas 3 ou 4 meios:
Ciclo (2 4 3)*
ciclo (2 3 4)*
Ciclo (1 9 3)**
Ciclo (1 3 9)**
(1 3)(2 4)
(1 4)(2 3)
* Você pode fazer esses algoritmos na face da frente ou de trás, usando rotações do cubo antes.
** Esse tipo de "algoritmo" é muito útil, desde que você saiba usá-lo :) Com esses dois exemplos acho que é possível "aprender". Você pode usá-lo em qualquer camada do meio, M, E ou S.
Eu coloquei alguns adicionais abaixo, que eu também uso, mas que não são totalmente necessários. Cique no [+] para ver.
Adicionais [+]
Ciclo (1 2 4)
Ciclo (1 4 2)
Aqui os setups são limitados nas faces direita e esquerda a meias-voltas, ou sejá, você só pode usar R2 ou L2 (e não R, R', L ou L').
Vamos ao exemplo, o mesmo scramble: L2 B D2 U' F U' B D2 B' D' B2 F2 D U B' L2 B2 U2 B' R' B D2 F2 R L2
Os meios, depois de orientados, ficam assim:
O primeiro ciclo é (1 11 3 7 6). O segundo, começando com o menor número não usado (2) fica (2 5 4 9 8 12 10).
A minha solução seria:
(1 11 3): M' B2 M B2
(1 7 6): U2 x' (R U' R U R U R U' R' U' R2) x U2
(2 5 4): F (R U' R U R U R U' R' U' R2) F'
(2 9 8): U' F' x (R2 U' R' U' R U R U R U' R) x' F U
(2 12 10): S' D2 S D2
Paridade de permutações
Em metade das vezes (teoricamente), você vai ter o que chamamos de "problema de paridade", ou simplesmente "paridade", que consiste em 2 cantos e 2 meios que "sobram". Depois de resolver todos os ciclos, ainda ficam 2 cantos a serem trocados entre si e 2 meios na mesma situação. Como não é possível trocar apenas 2 peças no cubo, existem algumas estratégias pra resolver essas situações:
A primeira estratégia é usar dois algoritmos "básicos", pra resolver cantos e meios "separadamente". Os dois mais usados são a permutação T (para os cantos) e a permutação H (para os meios).
Permutação T

R U R' U' R' F R2 U' R' U' R U R' F'
Permutação H

M2' U M2' U2 M2' U M2'
Você então faz setups para deixar os cantos nessas posições (UFR e UBR), faz a permutação T e desfaz os setups. Isso "conserta" os dois cantos, mas troca também 2 meios, UL e UR. Esses dois meios vão ser resolvidos com os outros 2 restantes, fazendo-se setups e a permutação H e desfazendo os setups.
Outra forma é resolver as 4 peças diretamente, usando qualquer das permutações que trocam 2 meios e 2 cantos. Aí é só usar setup moves pra deixar as peças erradas numa posição em que seja possível aplicar os algoritmos e depois desfazer os setups. Nem sempre é fácil fazer isso, então saber as duas estratégias é uma boa.

 possibilidades.
possibilidades.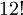 possibilidades.
possibilidades. possibilidades. O mesmo deve ocorrer com as arestas, pois aparecem mais
possibilidades. O mesmo deve ocorrer com as arestas, pois aparecem mais  possibilidades.
possibilidades. = 43.252.003.274.489.856.000
= 43.252.003.274.489.856.000








Nenhum comentário:
Postar um comentário